「人材の確保と育成」をテーマとしたJILPTの調査から、ものづくり産業における職人技の伝承方法2種類の方向性を示す指標を作ってみました。元になったクロス集計結果から因子分析を行って係数を決定。アンケートの回答割合から一次変換した数値を求めます。
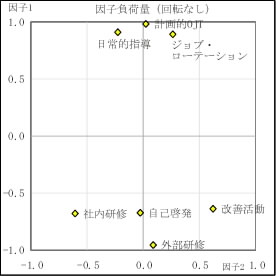
〔図2-1 因子負荷量(実施している教育訓練)〕
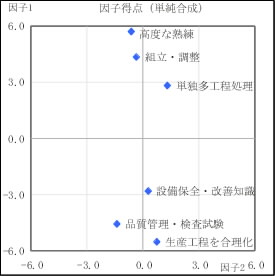
〔図2-2 因子得点(求めている知識・技能)〕
■「暗黙知そのままの伝達」と「形式知化による伝達」
前回の記事「技の伝承と人材育成1」で、JILPT(労働政策研究・研修機構)の調査「ものづくり産業における人材の確保と育成-機械・金属関連産業の現状-」という調査結果の一部を紹介しました。その中から岡目八目的に“勝手読み”して、技の伝承方法には大きく次の2種類があるとの仮説を立てました。
(A) 個人力:熟練技の直接的な伝承。現場作業を通じて伝える。暗黙知
(B) 集団力:技の標準化による伝承。文書化など共有財産にする。形式知
調査の中で、
(問1)「貴事業所では、技能系正社員にどのような知識・技能を求めていますか」
(問2)「貴事業所では、技能系正社員を対象にどのような教育訓練を実施していますか」(複数回答)
という問があり、それぞれの選択肢が(A群)(B群)それぞれに分類できそうだと推察しました。
(問1)
(A群)
(1)高度に卓越した熟練技能
(2)単独で多工程を処理する技能
(3)組立て・調整の技能
(B群)
(4)生産工程を合理化する知識・技能
(5)品質管理や検査・試験の知識・技能
(6)設備の保全や改善の知識・技能
(問2)
(A群)
[1]上司が部下を、先輩が後輩を日常的に指導
[2]指導者を決めるなど計画的OJTを実施
[3]やさしい仕事から難しい仕事へジョブ・ローテーションを実施
(B群)
[4]外部の教育訓練機関などが実施している研修を受講させる
[5]改善提案や小集団活動への参加を奨励
[6]定期的な社内研修を実施
[7]自己啓発を奨励し、支援体制をとっている
問1と問2のクロス集計の結果が調査報告書(図表7-1-2)に掲載されていて、(A群)同士または(B群)同士のクロス部分はポイントが平均より高く、異なる群同士のクロス部分はポイントが平均より低いまたは平均並みという結果になっていることから、この2群に分けることに意味がありそうだと判断しました。
■因子分析による軸の設定
ここで立てた仮説は、次の通りです。
《技の伝達には(A)(B)のやや異なる2つの方向性があり、そのどちらを重視しているかが時代環境や企業の業態などで異なる。その傾向を、アンケート結果から推測し、指標化できるのではないか》
指標化の準備として、多変量解析の一手法である「因子分析」を用い、クロス集計の結果(行列)を分析してみます。因子分析とは、大雑把に言うと、「複数の項目属性を持つデータ集合から、共通してあてはまる特定の方向性を見つけ出す手法」です。ここでは、先に仮説として挙げた「集団力←→個人力」という軸を数値的に見つけ出すことが狙いです(※1)。
実際に処理した結果が冒頭の図2-1と図2-2です(※2、※3)。いずれもくっきりした計算結果が出ました(※4、※5)。
図2-1は、データに隠れている最も重要な特性2つ(取り出された因子1と因子2)を切り出して、縦横2次元の表に問2の7つの選択肢(の因子負荷量)を配置した散布図です。図の上の方にある3つの要素と下の方にある4つの要素の2グループにくっきり分かれ、それぞれ(A群)と(B群)に該当します。
図2-2は、この因子に対して問1の6つの要素についての因子得点で散布図を作ったものです。これも予期した通り、(A群)3つと(B群)3つにくっきり分類できます。
ちなみに、散布図の横軸「因子2」は、因子1に次ぐなんらかの方向性が数値上で導かれたものです。因子2についても何らかの意味があるものかと少しいじってみましたが、結論としてはあまり意味のある軸ではないようです。もともとの仮説で1因子しか想定していませんでしたので、以下の議論では因子2以下は完全に捨てて、当初の狙いであった因子1のみに集中します(※6)。
■指標化の試み
さてここで、何らかの企業集団の問2に対する回答割合(0~100%)があったとします。選択肢[1]から[7]に対してそれぞれ
x1, x2, x3, x4, x5, x6, x7 (0 <= xn <=100) と書くことにします。 選択肢[1]から[7]に対応する因子負荷量(図2-1縦軸の数値)はそれぞれ a1(=0.91), a2(=0.98), a3(=0.89),
a4(=-0.95), a5(=-0.64), a6(=-0.68), a7(=-0.67)
です。
これらから次のような合成値Σaxを作ってみます。
Σax = a1x1 + a2x2 + … + a7x7
ようするに各因子負荷量でプラスマイナスの重みをつけて合計した数値です。
さらに、数字を整えるために一次変換をします。これは本質的な話ではなく、問1の因子得点(図2-2縦軸の数値)とスケールを合わせるためだけの変換です(※7)。
y = PΣax + Q (P=0.203、Q=-8.256)
これで、(x1, x2, … x7) → y と変換された指標ができました。
ざっくり言うと、
yがプラス方向に大きいほど「(A群) 個人力」重視
yがマイナス方向に大きいほど「(B群) 集団力」重視
と結論付けることができます。
たとえば調査全体(サンプル数2015件)についてyを計算すると、「-1.44」という数字になります。
y = 0.203×(0.91×61.5 + … -0.67×18.5) -8.256 = -1.44
なにやら難しい言葉や数式が並んでしまいましたが、あまり本気で考えすぎないでください(笑)。あくまでもある種の試みにすぎませんので…。
次回の記事で、この指標化と元調査の図表7-1-2から、実際に「何らかの企業集団」ごとの指標を計算してみます。
(続く)
【注】
※1 アンケート結果の多変量解析を行うとき、個々の回答のYes/Noを数字の「1」「0」に置き換えて分析することが多いかもしれません。しかしここでは、2000件以上の回答1件1件の結果が公表されているわけではありませんから、ある集団ごとの結果(クロス集計の結果)をもとに分析しているとお考えください。図表7-1-2のクロス集計の該当部分のみを分析に用いています。というより、このクロス集計行列の中に明確に「ある方向性」が隠れていることが想定できることから、今回の因子分析をやり始めたといった方が適切でしょう。
なお、問1は「3番目まで選べる」複数回答方式ですが、クロス集計では「最も重要なもの」として選んだ企業のみを集計対象としています。
※2 因子分析の計算に利用したソフトは、Excel2002およびそのアドインソフト「Excel多変量解析」(販売元:エスミ)の少し古いバージョン。
※3 今回の分析については、因子分析ではなく主成分分析で行っても似たような結果が得られます。
※4 因子分析の設定条件:計算する因子の数は「3」。共通性の初期値は「相関最大値」で「反復推定」。座標回転は「なし」。因子得点は「単純合成法」。
なお、一般的によく使われるバリマックス法で回転させると、図2-1全体が右45度くらいに動き、(A群)が右上に、(B群)が左下に集中する結果となります。本文で使っている「因子1」が2つの因子から構成されるとも読み取れますが、それは数字の“あや”のようなものだと判断しました。もともと1因子しか想定していないので、座標回転はせず主要因子1つが明確に現れるよう「回転なし」で軸を決めました。
※5 因子1の「寄与率」は68.8%
※6 (回転なし状態での)「因子2」を無理にみてみると、たとえば「単工程←→多工程」とかいった意味が見出せなくもありませんでしたが、それらを十分に裏付けるには至りませんでした。寄与率も12.6%と低いので、見捨てます。
※7 問1の6つの選択肢について(元調査の図表7-1-2から)Σaxの値を計算し、それが問1の因子得点(図2-1の縦軸の数値)に近似されるように回帰分析を行って、係数のPとQを算出しました。
